Leetcode Tree and Binary Tree
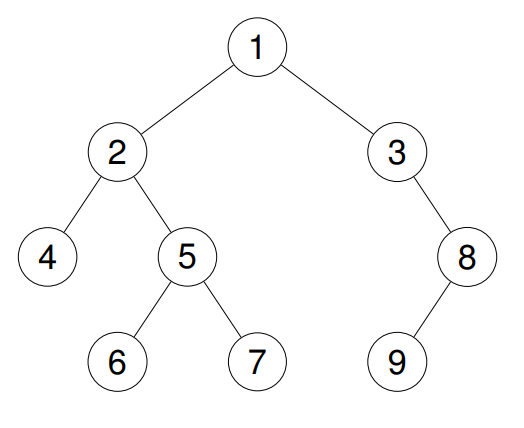
LeetCode 144. Binary Tree Preorder Traversal
Description
Given the root of a binary tree, return the preorder traversal of its nodes' values.
Solution one - Recursive
class Solution {
private List<Integer> list = new LinkedList<>();
public List<Integer> preorderTraversal(TreeNode root) {
// if root is null
if(root == null) {
List<Integer> list2 = new LinkedList<>();
return list2;
} else {
list.add(root.val);
}
// preorder traversal is root , left child, right child
if (root.left != null) preorderTraversal(root.left);
if (root.right != null) preorderTraversal(root.right);
return list;
}
}
Solution two - Stack
class Solution {
private List<Integer> list = new LinkedList<>();
public List<Integer> preorderTraversal(TreeNode root) {
// use stack
Stack<TreeNode> stack = new Stack<TreeNode>();
// if root is null
if(root == null) {
return list;
} else {
stack.push(root);
while(!stack.isEmpty()) {
TreeNode temp = stack.pop();
list.add(temp.val);
// 因为栈是先进后出,为了保证先序遍历根节点之后是先读取左子树的节点,所以左子树节点后进栈
if(temp.right != null) {
stack.push(temp.right);
}
if(temp.left != null) {
stack.push(temp.left);
}
}
}
return list;
}
}
LeetCode 94. Binary Tree Inorder Traversal
Description
Given the root of a binary tree, return the inorder traversal of its nodes' values.
Solution one - Resursive
class Solution {
List<Integer> list = new LinkedList<Integer>();
public List<Integer> inorderTraversal(TreeNode root) {
if( root == null) {
List<Integer> temp = new LinkedList<Integer>();
return temp;
}
// Inorder traversal: left child, root, right child
if(root.left != null) inorderTraversal(root.left);
list.add(root.val);
if(root.right != null) inorderTraversal(root.right);
return list;
}
}
Solution two - Stack
class Solution {
private List<Integer> list = new LinkedList<>();
public List<Integer> inorderTraversal(TreeNode root) {
// use stack
Stack<TreeNode> stack = new Stack<TreeNode>();
// if root is null
if(root == null) {
return list;
} else {
// 当栈不为空,或者当前节点不为空时继续遍历
while(root != null || !stack.isEmpty()) {
// 不断将左节点压入栈,直到最左边
while (root != null) {
stack.push(root);
root = root.left;
}
// 弹出栈顶元素,并存入列表
root = stack.pop();
list.add(root.val);
// 遍历当前节点右子树
root = root.right;
}
}
return list;
}
}
LeetCode 145. 二叉树的后序遍历
Description
给你一棵二叉树的根节点 root ,返回其节点值的 后序遍历 。
Solution one - Rescursive
class Solution {
List<Integer> list = new LinkedList<Integer>();
public List<Integer> postorderTraversal(TreeNode root) {
if(root == null) return new LinkedList<Integer>();
if(root.left != null) postorderTraversal(root.left);
if(root.right != null) postorderTraversal(root.right);
list.add(root.val);
return list;
}
}
LeetCode 701. 二叉树搜索树中的插入操作
Description
给定二叉搜索树(BST)的根节点 root 和要插入树中的值 value ,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ,新值和原始二叉搜索树中的任意节点值都不同。
Solution one - 通过递归找到值应该插入的位置
class Solution {
public TreeNode insertIntoBST(TreeNode root, int val) {
// 如果树为空,直接插入
if(root == null) {
root = new TreeNode(val);
} else {
if(val < root.val) {
root.left = insertIntoBST(root.left, val);
} else {
root.right = insertIntoBST(root.right, val);
}
}
return root;
}
}
LeetCode 700. 二叉搜索树中的搜索
Description
给定二叉搜索树(BST)的根节点 root 和一个整数值 val。
你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 null 。
Solution one - recursive
class Solution {
public TreeNode searchBST(TreeNode root, int val) {
// 递归到某结点,如果传进来的root为空,或者该节点的值就是要找的值,直接返回该节点
if(root == null || root.val == val) return root;
if(root.val < val) {
// 该节点的值小于要找的值,递归右子树
root = searchBST(root.right, val);
} else {
root = searchBST(root.left, val);
}
return root;
}
}
LeetCode 450. 删除二叉搜索树中的节点
Description
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
- 首先找到需要删除的节点;
- 如果找到了,删除它。
Solution one
思路:找到删除的结点可以使用递归找到该节点,但是删除了该节点之后,二叉搜索树变成了什么样子?
- 如果删除的是叶子结点,直接删除
- 如果删除的不是叶子结点,为保持二叉搜索树的性质,可以找该节点的左子树中的最大节点,或者右子树的最小节点,替换掉该节点,
- 删除节点只有左子树,将左子树作为新的子树,返回要删除节点的左孩子
- 删除节点只有右子树,将右子树作为新的子树,返回要删除节点的右孩子
- 删除节点左右孩子都有
- 找到左子树中的最大节点,这个左子树最大节点一定没有右孩子,在这个左子树中最大节点调用删除递归,并返回值,然后更新root并返回
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
// 1. 如果删除的是叶子结点,直接删除
// 2. 如果删除的不是叶子结点,为保持二叉搜索树的性质,可以找该节点的左子树中的最大节点,或者右子树的最小节点,替换掉该节点,
// 1. 删除节点只有左子树,将左子树作为新的子树,返回要删除节点的左孩子
// 2. 删除节点只有右子树,将右子树作为新的子树,返回要删除节点的右孩子
// 3. 删除节点左右孩子都有
// 1. 找到左子树中的最大节点,这个左子树最大节点一定没有右孩子,在这个左子树中最大节点调用删除递归,并返回值,然后更新root并返回
// 处理空树
if(root == null) return root;
// 找到要删除的节点
if(root.val < key) {
root.right = deleteNode(root.right, key);
return root;
}
if(root.val > key) {
root.left = deleteNode(root.left, key);
return root;
}
if(root.val == key) {
if(root.left == null && root.right == null) { return null;}
if(root.left != null && root.right == null) { return root.left; }
if(root.left == null && root.right != null) { return root.right; }
if(root.left != null && root.right != null) {
// 找到左子树的最大节点,再递归左子树
TreeNode temp = root.left;
while(temp.right != null) {
temp = temp.right;
}
root.left = deleteNode(root.left, temp.val); // 删除左子树最大节点
temp.left = root.left; // 左子树最大节点值,替换key值
temp.right = root.right;
return temp;
}
}
return root;
}
}
LeetCode 104. 二叉树的最大深度
Description
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
Solution one - BFS 层次遍历
遍历每一层,路径上节点数+1
class Solution {
public int maxDepth(TreeNode root) {
int depth = 0;
if(root == null) return depth;
Queue<TreeNode> dq = new LinkedList<TreeNode>();
dq.add(root);
while(!dq.isEmpty()) {
int size = dq.size();
for(int i = 0; i < size; i++) {
TreeNode temp = dq.poll();
if(temp.left != null) dq.add(temp.left);
if(temp.right != null) dq.add(temp.right);
}
depth++;
}
return depth;
}
}
Solution two - DFS Recursive
class Solution {
int res = 0;
public int maxDepth(TreeNode root) {
// DFS
if(root == null) return 0;
int leftHeight = maxDepth(root.left);
int rightHeight = maxDepth(root.right);
return Math.max(leftHeight, rightHeight) + 1;
}
}